On Thinking

I've started realizing that my mathematical fundamentals have become weak; I suspect they might never have been as strong as I imagined in the first place.

A simple example of an incorrect assumption I've had for a long time: that \((p_1 * p_2 * p_3 *... * p_n) + 1\) is always a prime. \(2*3*5*7*11*13 + 1 = 30031\) is \(59^2\).

Mathematics requires precision: which is what requires mathematical notation, and paying attention to precision of language (and no head injuries).

Notation in mathematics relies on stripped down versions of words used in common language:

• and, or \(\land\) is strictly used to combine the truth values of 2 statements, and doesn't hold any meaning around consequence or ordering.
• or, or \(\lor\) means an inclusive or, and not the exclusive ("either") or.
• not, or \(\lnot\) is true negation; it cannot be used loosely.
• Implies includes both causal and truth-value conditional between the antecedent and the consequent.
• The conditional is represented by \(\implies\), which attaches no direct meaning to the antecedent or consequent; they need not be related.

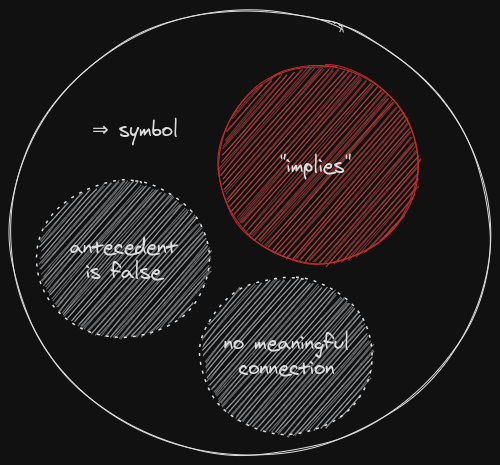
• The truth table for implies is meaningful when there is a true antecedent; it's somewhat meaningless for a false antecedent and is defined by looking at the inverse.
• Equivalence is when \(\phi\) implies \(\psi\) and \(\psi\) implies \(\phi\); it's also referred to as "iff", or "if and only if".
• \(\forall\) and \(\exists\) help define the context for statements, and must be applied carefully in the correct order.

After explaining the combinators and quantifiers, the author moves on to proofs. Proofs are essentially a collection of arguments that validate a statement in incremental steps.

A proof servers 2 purposes

• Evaluating if a statement is correct
• Communicating the correctness of the statement to others

While it's a very bad idea to fit every problem to a template, there are patterns that can be applied to construct proofs:

• Proof by Contradiction: To prove \(\phi\), assume \(\neg\phi\) and reach a point that is obviously false. This proves \(\neg\phi => F\), which is the contrapositive to \(T => \phi\); or \(\phi\) is true.
• Proving Conditionals: To prove \(\phi => \psi\), assume \(\phi\) and derive $ψ$\.
• Proving Quantified Statements: Solve these either directly or by contrapositive, whichever proves to be simpler.
• Proof by induction: Assume \(f(n)\), and derive \(f(n + 1)\).

(I have to admit that I kept thinking of the similarities to programs throughout this section: programs tell computers what to do, and humans what they do; and applying patterns to programming makes the process all the more simpler.)

There are several fascinating anecdotes in this book around actually reasoning about the world: starting with the famous example of adding armor to aircraft where there aren't bullet holes.

I've always been skeptical of claiming to understand an algorithm without actually implementing it; the same applies to every other endeavor to learn – and is beautifully captured by a quote I first came across in this book: No ideas but in things.

I read Polya's book on tackling problems when I was in high school, and I've relied on the heuristics from the book ever since. The core of the book is around 4 ideas:

• Understand the problem
• Create a plan
• Execute the plan
• Review the solution

The book then goes into various heuristics that help in approaching problems; I also found it very valuable to think about metacognition.

In retrospect, my note about debugging was probably inspired by How to Solve it without consciously realizing it.

I realized that simply sketching things out was extremely valuable to be able to think things through. Feynman diagrams are one example of notation that help with thinking.

Searching for thinking with drawing lead me to this book; it's a bit more business-y than I'm used to, but seems interesting nevertheless.

Systemantics is one of the most fascinating books I've read.

I've referred to Small Gods by Terry Pratchett as one of my favorite books of all time because of the core message of the book – to pay deep attention to the heart of everything and avoid getting distracted by appearances. System-Antics reinforced this principle, and also shows how appearances can become more important than the core function of a system and take it over.